https://www.youtube.com/watch?v=xE3ZKkaqdUA
https://www.youtube.com/watch?v=eU2mT2hlnsY








1. Problem: Find the value of c.Solution: a2 + b2 = c2 Write the Pythagorean Theorem and then plug in any given information. 52 + 122 = c2 The information that was given in the figure was plugged in. 169 = c2 Solve for c c = 13
 Ba
Ba 
 sine of angle A = (measure of opposite leg)/(measure of hypotenuse). In the figure, the sin of angle A = (a/c).
sine of angle A = (measure of opposite leg)/(measure of hypotenuse). In the figure, the sin of angle A = (a/c). 1. Problem: Find sin A, cos A, and tan A.
 Solution: sine = (opposite/hypotenuse)
sine = 5/13
cosine = (adjacent/hypotenuse)
cos = 12/13
tangent = (opposite/adjacent)
tan = 5/12
Solution: sine = (opposite/hypotenuse)
sine = 5/13
cosine = (adjacent/hypotenuse)
cos = 12/13
tangent = (opposite/adjacent)
tan = 5/12
Be aware that, although the example above seems to indicate otherwise, the values for the trigonometric ratios depend on the measure of the angle, not the measures of the triangle's sides. 1. Problem: A ladder 12 meters long leans
against a building. It rests on
the wall at a point 10 meters
above the ground. Find the angle
the ladder makes with the ground.
Solution: Make sure you know what is being
asked. Then use the given
information to draw and label a
figure. Here's our idea of a
figure for this problem:
 Choose a variable to represent the
measure of the angle you are asked
to find. Using the variable you
have chosen, write an equation that
will solve the problem.
sin x2 = (10/12)
The above equation is derived from
the given information and the
knowledge of the sine
ratio.
Find the solution using a calculator's
Arcsine function or a table
of trigonometric ratios.
TI-82 screen: sin-1 (10/12) = 56.44
Trigonometric Ratios Table:
sin 56o = 0.8290
sin 57o = 0.8387
By either answer, after rounding to
the nearest degree, the answer is 56o.
Choose a variable to represent the
measure of the angle you are asked
to find. Using the variable you
have chosen, write an equation that
will solve the problem.
sin x2 = (10/12)
The above equation is derived from
the given information and the
knowledge of the sine
ratio.
Find the solution using a calculator's
Arcsine function or a table
of trigonometric ratios.
TI-82 screen: sin-1 (10/12) = 56.44
Trigonometric Ratios Table:
sin 56o = 0.8290
sin 57o = 0.8387
By either answer, after rounding to
the nearest degree, the answer is 56o.
Youtube Video:
ADVERTISEMENT
| |
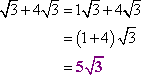
![3 sqrt[8] + 5 sqrt[2] = 3 sqrt[(2 * 2) * 2] + 5 sqrt[2] = 3 * 2 sqrt[2] + 5 sqrt[2] = 6 sqrt[2] + 5 sqrt[2] = 11 sqrt[2]](http://www.purplemath.com/modules/radicals/rad053.gif)
 = 3 sqrt[2] + sqrt[2 * 3] = 3 sqrt[2] + sqrt[6]](http://www.purplemath.com/modules/radicals/rad059.gif)
![(1 + sqrt[2])(3 - sqrt[2]) = -1sqrt[2] - sqrt[2]sqrt[2] + 3 + 3sqrt[2] = 3 + 2sqrt[2] - sqrt[2 * 2]](http://www.purplemath.com/modules/radicals/rad061.gif)
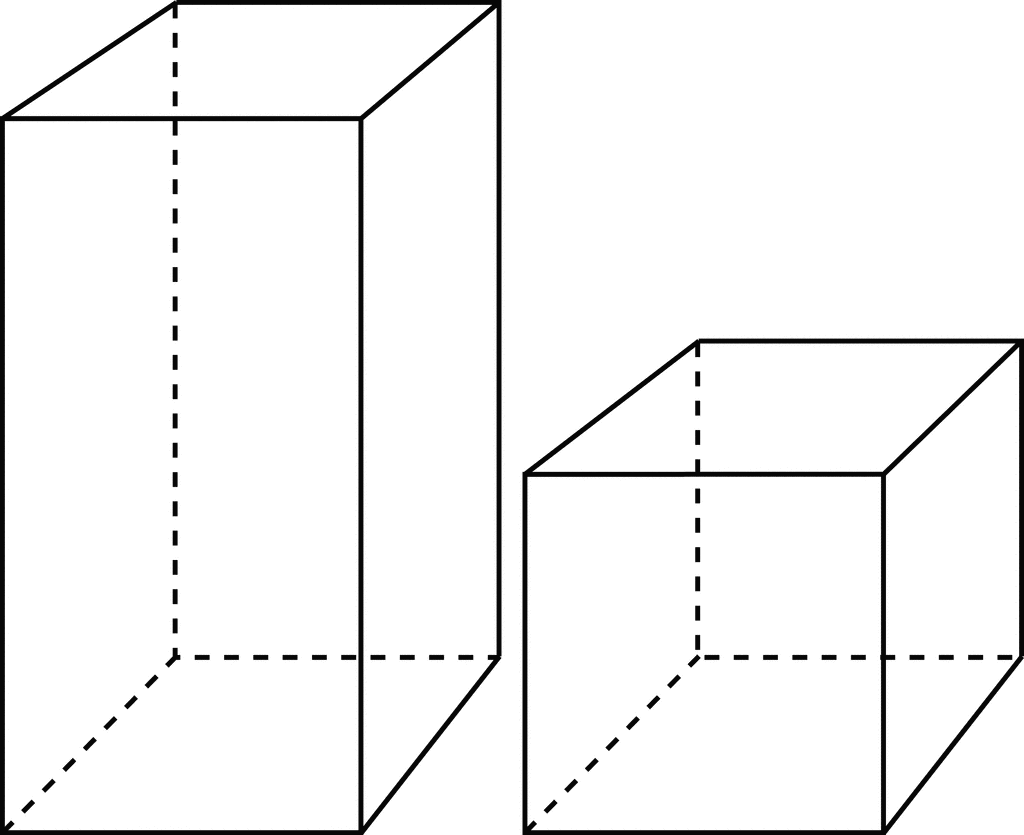
| 1. Simplify | Answer: | |||
| 2. Simplify | Answer: | |||
| 3. Since the radicals in steps 1 and 2 are now the same, we can combine them. | Answer: | |||
| 4. After combining, you are left with: | Answer: | |||
| 5. Can you combine these radicals? | Answer: NO | |||
| 6. Therefore, | ||||